El muestreo es una herramienta de la investigación científica. Su función básica es determinar que parte de una realidad en estudio (población o universo) debe examinarse con la finalidad de hacer inferencias sobre dicha población. El error que se comete debido a hecho de que se obtienen conclusiones sobre cierta realidad a partir de la observación de sólo una parte de ella, se denomina error de muestreo. Obtener una muestra adecuada significa lograr una versión simplificada de la población, que reproduzca de algún modo sus rasgos básicos.
Muestra: En todas las ocasiones en que no es posible o conveniente realizar un censo, lo que hacemos es trabajar con una muestra, entendiendo por tal una parte representativa de la población. Para que una muestra sea representativa, y por lo tanto útil, debe de reflejar las similitudes y diferencias encontradas en la población, ejemplificar las características de la misma.
Tipos de Muestreo
Inferencia estadística
Muestreo probabilístico
Muestreo aleatorio simple
Muestreo aleatorio sistemático
Se elige un individuo al azar y a partir de él, a intervalos constantes, se eligen los demás hasta completar la muestra.Por ejemplo si tenemos una población formada por 100 elementos y queremos extraer una muestra de 25 elementos, en primer lugar debemos establecer el intervalo de selección que será igual a 100/25 = 4. A continuación elegimos el elemento de arranque, tomando aleatoriamente un número entre el 1 y el 4, y a partir de él obtenemos los restantes elementos de la muestra.
2, 6, 10, 14,..., 98
Muestreo aleatorio estratificado
Se divide la población en clases o estratos y se escoge, aleatoria mente, un número de individuos de cada estrato proporcional al número de componentes de cada estrato.En una fábrica que consta de 600 trabajadores queremos tomar una muestra de 20. Sabemos que hay 200 trabajadores en la sección A, 150 en la B, 150 en la C y 100 en la D.Teorema del Límite Central
El teorema del límite central o teorema central del límite indica que, en condiciones muy generales, si Sn es la suma de n variables aleatorias independientes, entonces la función de distribución de Sn «se aproxima bien» a una distribución normal (también llamada distribución gaussiana, curva de Gauss o campana de Gauss). Así pues, el teorema asegura que esto ocurre cuando la suma de estas variables aleatorias e independientes es lo suficientemente grande.
Definición
Sea  la función de densidad de la distribución normal definida como
la función de densidad de la distribución normal definida como
 la función de densidad de la distribución normal definida como
la función de densidad de la distribución normal definida como
con una media µ y una varianza σ2. El caso en el que su función de densidad es  , a la distribución se le conoce como normal estándar.
, a la distribución se le conoce como normal estándar.
 , a la distribución se le conoce como normal estándar.
, a la distribución se le conoce como normal estándar.
Se define Sn como la suma de n variables aleatorias, independientes, idénticamente distribuidas, y con una media µ y varianza σ2 finitas (σ2≠0):
de manera que, la media de Sn es n·µ y la varianza n·σ2, dado que son variables aleatorias independientes. Con tal de hacer más fácil la comprensión del teorema y su posterior uso, se hace una estandarización de Sn como
para que la media de la nueva variable sea igual a 0 y la desviación estándar sea igual a 1. Así, las variables Zn convergerán en distribución a la distribución normal estándar N(0,1), cuando n tienda a infinito. Como consecuencia, si Φ(z) es la función de distribución de N(0,1), para cada número real z:
donde Pr( ) indica probabilidad y lim se refiere a límite matemático.

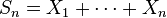


No hay comentarios:
Publicar un comentario