miércoles, 13 de junio de 2012

La Probabilidad


Definición de probabilidad

La probabilidad de un suceso es un número, comprendido entre 0 y 1, que indica las posibilidades que tiene de verificarse cuando se realiza un experimento aleatorio.

Experimentos deterministas



Son los experimentos de los que podemos predecir el resultado antes de que se realicen.
Ejemplo
Si dejamos caer una piedra desde una ventana sabemos, sin lugar a dudas, que la piedra bajará. Si la arrojamos hacia arriba, sabemos que subirá durante un determinado intervalo de tiempo; pero después bajará.

Experimentos aleatorios

Son aquellos en los que no se puede predecir el resultado, ya que éste depende del azar.
Ejemplos
Si lanzamos una moneda no sabemos de antemano si saldrá cara o cruz.
Si lanzamos un dado tampoco podemos determinar el resultado que vamos a obtener.



Teoría de probabilidades


La teoría de probabilidades se ocupa de asignar un cierto número a cada posible resultado que pueda ocurrir en un experimento aleatorio, con el fin de cuantificar dichos resultados y saber si un suceso es más probable que otro. Con este fin, introduciremos algunas definiciones:


Suceso


Es cada uno de los resultados posibles de una experiencia aleatoria.

Al lanzar una moneda salga cara.

Al lanzar una moneda se obtenga 4.

Espacio muestral


Es el conjunto de todos los posibles resultados de una experiencia aleatoria, lo representaremos por E (o bien por la letra griega Ω).

Espacio muestral de una moneda:

E = {C, X}.

Espacio muestral de un dado:

E = {1, 2, 3, 4, 5, 6}.

Suceso aleatorio

Suceso aleatorio es cualquier subconjunto del espacio muestral.
Por ejemplo al tirar un dado un suceso sería que saliera par, otro, obtener múltiplo de 3, y otro, sacar 5.

Ejemplo

Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas. Calcular:
1. El espacio muestral.
E = {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b); (n, n,n)}
2. El suceso A = {extraer tres bolas del mismo color}.
A = {(b,b,b); (n, n,n)}
3. El suceso B = {extraer al menos una bola blanca}.
B= {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b)}
4. El suceso C = {extraer una sola bola negra}.
C = {(b,b,n); (b,n,b); (n,b,b)}

Diagrama de árbol

Un diagrama de árbol es una representación gráfica que muestra los resultados posibles de una serie de experimentos y sus respectivas probabilidades.

Ejemplo1

Experimento: Se lanza una moneda, si sale águila se lanza un dado y si sale sol se lanza la moneda de nuevo.

Concepto clásico de Probabilidad

Este enfoque permite determinar valores de probabilidad antes de ser observado el experimento por lo que se le denomina enfoque a priori.
El enfoque clásico es aplicado cuando todos los resultados son igualmente probables y no pueden ocurrir al mismo tiempo.
Si queremos conocer la probabilidad del evento A según este enfoque debemos calcular el siguiente cociente:
                           N(A)
               P(A) = -------------
                           N(S)
Donde:
N(A): resultados elementales posibles son favorables en el evento A
N(S): posibles resultados en el espacio muestral
EJEMPLOS
1) En un mazo de cartas bien barajadas que contiene 4 ases y 48 cartas de otro tipo, la probabilidad de obtener un as (A) en una sola extracción es
            N(A)            4        1
              P(A) =   ------   =    -----  =  ----
           N(S)            52      13
2) El experimento es lanzar un dado. ¿Cuál es la probabilidad de que caiga un dos hacia arriba?
          P( caiga 2 ) =       1      =       .166
                                     ----
                                      6            

ENFOQUE DE FRECUENCIAS RELATIVAS (a posteriori o empírico)

Este enfoque permite determinar la probabilidad con base en la proporción de veces que ocurre un resultado favorable en cierto número experimentos.
No implica ningún supuesto previo de igualdad de probabilidades.
A este enfoque se le denomina también enfoque empírico debido a que para determinar los valores de probabilidad se requiere de la observación y de la recopilación de datos. También se le denomina a posteriori, ya que el resultado se obtiene después de realizar el experimento un cierto número de veces.
Si queremos conocer la probabilidad del evento A según este enfoque debemos calcular el siguiente cociente:
            Número de observaciones de A        n(A)
P(A) = -------------------------------------- = -------
               Tamaño de la muestra               n
EJEMPLOS
1) Antes de incluir la cobertura para ciertos tipos de problemas dentales en pólizas de seguros médicos para adultos con empleo, una compañía de seguros desea determinar la probabilidad de ocurrencia de esa clase de problemas, para que pueda fijarse la prima de seguros de acuerdo con esas cifras. Por ello, un especialista en estadística recopila datos para 10,000 adultos que se encuentran en las categorías de edad apropiadas y encuentra que 100 de ellos han experimentado el problema dental específico durante el año anterior.
Por ello, la probabilidad de ocurrencia es:
            100
P(A) = --------------- = 0.01, o 1%
10,000
2) Se sabe que una moneda está cargada. Para determinar la probabilidad de que caiga águila se lanza 60 veces la moneda al aire, de las cuales 25 veces cayó águila. Si aplicamos la fórmula:
      P ( cae águila ) = 25 = 0.41
                                ----------  
                                   60

 ENFOQUE SUBJETIVO DE LA PROBABILIDAD (personalista)
Se diferencia de lo dos enfoques anteriores, debido a que tanto el enfoque clásico como el de frecuencia relativa producen valores de probabilidad objetivos.
El enfoque señala que la probabilidad de un evento es el grado de confianza que una persona tiene en que el evento ocurra, con base en toda la evidencia que tiene disponible, fundamentado en la intuición, opiniones, creencias personales y otra información indirecta.
Este enfoque no depende de la repetitividad de ningún evento y permite calcular la probabilidad de sucesos únicos y se da el caso de que ocurra o no esa única vez.
Debido a que el valor de la probabilidad es un juicio personal, al enfoque subjetivo se le denomina también enfoque personalista.
EJEMPLOS
1) Hay una probabilidad del 80% de que el América le gane a las Chivas.
2) Hay una probabilidad del 90% de que las ventas mejoren el año próximo
3) Hay una alta probabilidad de sacarme un 100.
4) A causa de los impuestos y de otros posibles usos de sus fondos, un inversionista ha determinado que la compra de terrenos sólo se justifica si existe al menos una probabilidad de 0.90 de que los terrenos aprecien su valor en 50% o más en los cuatro años siguientes. Al evaluar cierto terreno, este inversionista estudia los cambios de precio en el área en los años recientes, considera los niveles de precios vigentes, estudia la situación imperante y probablemente futura de proyectos de desarrollo urbano y consulta las estadísticas sobre el desarrollo económico del área geográfica en general. Con base en este recuento, concluye que existe una probabilidad de alrededor de 0.75 de que efectivamente ocurra la requerida apreciación de valor. Puesto que este valor de probabilidad en inferior a la probabilidad mínima requerida de 0.90

TIPOS DE EVENTOS


-Exhaustivos.- Se dice que dos o más eventos son exhaustivos si se consideran todos los posibles resultados.

-No exhaustivos.- Se dice que dos o más eventos son no exhaustivos si no agotan todos los posibles resultados.

-Mutuamente exclusivos.- Eventos que no pueden ocurrir en forma simultánea.

-No mutuamente exclusivos.- Eventos que pueden ocurrir en forma simultánea.

-Independientes.- eventos cuya probabilidad no es afectada porque ocurran o no ocurran entre ellos.

-Dependientes.- Eventos cuya probabilidad cambia dependiendo de que ocurran o no ocurran entre si.

PRINCIPIO FUNDAMENTAL DE CONTEO
Permutaciones
El número de Permutaciones de n objetos es el número de formas en los que pueden acomodarse esos objetos en términos de orden.
Permutaciones En n Objetos
Permutaciones de n elementos tomando n a la vez es igual a:
nPn = n! = (n) x (n-1) x… x (2) x (1)
Ejemplo
Los cinco individuos que componen la dirección de una pequeña empresa manufacturera serán sentados juntos en un banquete. Determinar el número de diferentes posiciones posibles de los asientos para los cinco individuos.
Solución
n Pn = n! = 5! = (5)(4)(3)(2)(1) = 120
Permutaciones En Subgrupo De n Objetos
El número de permutaciones de n objetos tomados r a la vez, donde r es menor que n es igual a:
                 nPr =    n!
                            ----
                          (n-r)!
Ejemplo
En relación al ejemplo anterior, supongamos que sólo a tres de los cinco directivos se les pedirá representar a la compañía en el banquete. ¿Cuántas diferentes posiciones serán posibles en la mesa considerando que pueden ser elegidos tres cualesquiera de los cinco individuos?
Solución
n Pr = 5 P3 = n! = 5! = (5)(4)(3)(2)(1) = 6
                     ---- ---- ----------------
                    (n - r)!   (5 - 3)!        (2)(1)



Combinaciones



En el caso de las combinaciones, lo importante es el número de agrupaciones diferentes de objetos que pueden incurrir sin importar su orden.

Por lo tanto en las combinaciones se busca el número se subgrupos diferentes que pueden tomarse a partir de n objetos.

El número de combinaciones de n objetos tomados r a la vez es igual a:


                nCr =      n! 


                             ----
                         r! (n-r)! 




Ejemplo





Supongamos que se elegirá a tres miembros de una pequeña organización social con un total de diez miembros para que integren un comité. ¿Cuál es el número de grupos diferentes de tres personas que pueden ser elegidos, sin importar el diferente orden en el que cada grupo podría elegirse?





Solución



nCr =10C3 = n! = 10! =10×9x8×7!=10×9x8=720= 120


                -------     -------  --------- ------ ---
                   r(n - r)!   3!(10–3)!   3!x7!    3×2x1  6




Combinaciones representando la probabilidad





En términos de combinaciones, frecuentemente podemos determinar la probabilidad de un evento determinado, el número de combinaciones de resultados que incluyen ese evento en comparación con el número total de combinaciones posibles.






Los Axiomas De Probabilidad 



Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función definida sobre un conjunto de sucesos determine consistentemente sus probabilidades. Fueron formulados por kolmogórov en 1933.




Axiomas de Kolmogórov




Dado un conjunto de sucesos elementales, Ω, sobre el que se ha definida una σ-álgebra, σ de subconjuntos de Ω y una función P que asigna valores reales a los miembros de σ, a los que denominamos "sucesos", se dice que P es una probabilidad sobre (Ω,σ) si se cumplen los siguientes tres axiomas.

Primer axioma


La probabilidad de un suceso  A  es un número real mayor o igual que 0.


P(A) \geq 0  








Segundo axioma






La probabilidad del total, \Omega, es igual a 1, es decir,


P(\Omega) = 1\!



Tercer axioma


Si A_1, A_2, \dots son sucesos mutuamente excluyentes (incompatibles dos a dos, disjuntos o de intersección vacía dos a dos), entonces:




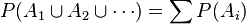P(A_1 \cup A_2 \cup \cdots) = \sum P(A_i).



Según este axioma se puede calcular la probabilidad de un suceso compuesto de varias alternativas mutuamente excluyentes sumando las probabilidades de sus componentes.





En términos más formales, una probabilidad es una medida sobre una σ-álgebra de subconjuntos del espacio muestral, siendo los subconjuntos miembros de la σ-álgebra los sucesos y definida de tal manera que la medida del total sea 1. Tal medida, gracias a su definición matemática, verifica igualmente los tres axiomas de Kolmogórov. A la terna formada por el espacio muestral, la σ-álgebra y la función de probabilidad se la denomina Espacio probabilístico, esto es, un "espacio de sucesos" (el espacio muestral) en el que se han definido los posibles sucesos a considerar (la σ-álgebra) y la probabilidad de cada suceso (la función de probabilidad).



Propiedades que se deducen de los axiomas



De los axiomas anteriores se deducen otras propiedades de la probabilidad:



    

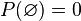  1.  P(\varnothing)=0 donde el conjunto vacío (\varnothing) representa en probabilidad el suceso imposible
    2. 

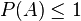
  2. Para cualquier suceso  P(A) \leq 1 
    3. 

  3.  P(A^c)=1-P(A)\;\!
    4. 

  4. Si  A \subseteq B entonces P(A) \leq P(B)
    5. 

  5.  P(A \cup B)= P(A) + P(B) - P(A \cap B)
    6. 




Teorema de Bayes



En la teoría de la probabilidad el teorema de Bayes es un resultado enunciado por Thomas Bayes en 1763 que expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A.



En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de A dado B con la probabilidad de B dado A. Es decir que sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber -si se tiene algún dato más-, la probabilidad de tener gripe si se tiene un dolor de cabeza, muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene vinculación íntima con la comprensión de la probabilidad de aspectos causales dados los efectos observados.








Sea 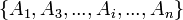\{A_1, A_3, ..., A_i,   ...,   A_n\} un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales P(B | A_i). Entonces, la probabilidad P(A_i | B) viene dada por la expresión:
P(A_i|B) = \frac{P(B | A_i) P(A_i)}{P(B)}



donde:


    

  • P(A_i) son las probabilidades a priori.
    • 

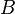  • P(B|A_i) es la probabilidad de B en la hipótesis A_i.
    • 

  • P(A_i|B) son las probabilidades a posteriori.
    •
Publicado por en

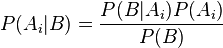
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)