Estadistica No Parametrica

La estadística no paramétrica es una rama de la estadística que estudia las pruebas y modelos estadísticos cuya distribución subyacente no se ajusta a los llamados criterios paramétricos. Su distribución no puede ser definida a priori, pues son los datos observados los que la determinan. La utilización de estos métodos se hace recomendable cuando no se puede asumir que los datos se ajusten a una distribución conocida, cuando el nivel de medida empleado no sea, como mínimo, de intervalo.

Las principales pruebas no paramétricas son las siguientes:

• Prueba χ² de Pearson
• Prueba binomial
• Prueba de Anderson-Darling
• Prueba de Cochran
• Prueba de Cohen kappa
• Prueba de Fisher
• Prueba de Friedman
• Prueba de Kendall
• Prueba de Kolmogórov-Smirnov
• Prueba de Kruskal-Wallis
• Prueba de Kuiper
• Prueba de Mann-Whitney o prueba de Wilcoxon
• Prueba de McNemar
• Prueba de la mediana
• Prueba de Siegel-Tukey
• Coeficiente de correlación de Spearman
• Tablas de contingencia
• Prueba de Wald-Wolfowitz
• Prueba de los signos de Wilcoxon

La mayoría de estos test estadísticos están programados en los paquetes estadísticos más frecuentes, quedando para el investigador, simplemente, la tarea de decidir por cuál de todos ellos guiarse o qué hacer en caso de que dos test nos den resultados opuestos. Hay que decir que, para poder aplicar cada uno existen diversas hipótesis nulas que deben cumplir nuestros datos para que los resultados de aplicar el test sean fiables. Esto es, no se puede aplicar todos los test y quedarse con el que mejor convenga para la investigación sin verificar si se cumplen las hipótesis necesarias. La violación de las hipótesis necesarias para un test invalidan cualquier resultado posterior y son una de las causas más frecuentes de que un estudio sea estadísticamente incorrecto. Esto ocurre sobre todo cuando el investigador desconoce la naturaleza interna de los test y se limita a aplicarlos sistemáticamente

PRUEBA BINOMIAL

La prueba binomial analiza variables dicotómicas y compara las frecuencias observadas en cada categoría con las que cabría esperar según una distribución binomial de parámetro 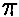especificado en la hipótesis nula tal como se ha explicado en elcapítulo anterior *.

La secuencia para realizar este contraste es:

Analizar

Pruebas no paramétricas

Binomial

Escalas de medición

Escalas de medición son una sucesión de medidas que permiten organizar datos en orden jerárquico. Las escalas de medición, pueden ser clasificadas de acuerdo a una degradación de las características de las variables.

Estas escalas son: nominales, ordinales, intervalares o racionales. Según pasa de una escala a otra el atributo o la cualidad aumenta.

 Las escalas de medición ofrecen información sobre la clasificación de variables discretas o continuas, tambien mas conocidas como escalas grandes o pequeñas. Toda vez que dicha clasificación determina la selección de la gráfica adecuada.

Prueba de la mediana

 

La prueba de la mediana es una prueba no paramétrica que podemos considerar un caso especial de la prueba de chi-cuadrado, pues se basa en esta última.

Su objetivo es comparar las medianas de dos muestras y determinar si pertencen a la misma población o no.

Para ello, se calcula la mediana de todos los datos conjuntamente. Después, se divide cada muestra en dos subgrupos: uno para aquellos datos que se sitúen por encima de la mediana y otro para los que se sitúen por debajo.

 La prueba de chi-cuadrado determinará si las frecuencias observadas en cada grupo difieren de las esperadas con respecto a una distribución de frecuencias que combine ambas muestras.

Esta prueba está especialmente indicada cuando los datos sean extremos o estén sesgados.

PRUEBA DE WILCOXON

Sea X una variable aleatoria continua. Podemos plantear cierta hipótesis sobre la mediana de dicha variable en la población, por ejemplo, M=M0. Extraigamos una muestra de tamaño m y averigüemos las diferencias Di = X - M0. Consideremos únicamente las n diferencias no nulas (n " m). Atribuyamos un rango u orden (0i) a cada diferencia según su magnitud sin tener en cuenta el signo.

Sumemos por un lado los 0+i , rangos correspondientes a diferencias positivas y por otro lado los 0-i , rangos correspondientes a diferencias negativas.

La suma de los órdenes de diferencias positivas sería igual a la suma de los órdenes de diferencias negativas, caso que la mediana fuera el valor propuesto M0. En las muestras, siendo M0 el valor de la verdadera mediana, aparecerán por azar ciertas discrepancias, pero si la suma de los rangos de un ciclo es considerablemente mayor que la suma de los rangos de otro signo, nos hará concebir serias dudas sobre la veracidad de M0.

La prueba de Wilcoxon va a permitir contrastar la hipótesis de que una muestra aleatoria procede de una población con mediana M0. Además, bajo el supuesto de simetría este contraste se puede referir a la media, E(X). Esta prueba es mucho mas sensible y poderosa que la prueba de los signos; como se puede apreciar utiliza mas información, pues no solo tiene en cuenta si las diferencias son positivas o negativas, sino también su magnitud.

El contraste de Wilcoxon puede ser utilizado para comparar datos por parejas. Supongamos que la distribución de las diferencias es simétrica, y nuestro propósito es contrastar la hipótesis nula de que dicha distribución está centrada en 0. Eliminando aquellos pares para los cuales la diferencia es 0 se calculan los rangos en orden creciente de magnitud de los valores absolutos de las restantes diferencias. Se calculan las sumas de los rangos positivos y negativos, y la menor de estas sumas es el estadístico de Wilcoxon. La hipótesis nula será rechazada si T es menor o igual que el valor correspondiente.

Si el número n de diferencias no nulas es grande y T es el valor observado del estadístico de Wilcoxon los siguientes contrastes tienen nivel de significación .

Si la hipótesis alternativa es unilateral, rechazaremos la hipótesis nula si

T - µT

--------- < -Z

T

Si la hipótesis alternativa es bilateral, rechazaremos la hipótesis nula si

T - µT

--------- < -Z /2

T

EJEMPLO

La salud mental de la población activa de sujetos de 60 años tiene

una mediana de 80 en una prueba de desajuste emocional (X). Un psicólogo cree que tras el retiro (jubilación) esta población sufre desajustes emocionales. Con el fin de verificarlo, selecciona al azar una muestra de sujetos retirados, les pasa la prueba de desajuste y se obtienen los siguientes resultados:

X: 69,70,75,79,83,86,88,89,90,93,96,97,98,99

¿Se puede concluir, con un nivel de significación de 0,05, que tras el retiro aumenta el promedio de desajuste emocional?

1.-

H0: M " 80 La población no incrementa su promedio de desajuste.

H1: M > 80 La población aumenta su nivel de desajuste tras el retiro.

2.- Suponemos que la muestra es aleatoria, la variable es continua y el nivel de medida de intervalo.

3.- Aunque la muestra es pequeña usemos los dos estadísticos:

Averigüemos Di = X - 80 y ordenemos las | Di |:

Di = -11, -10, -5, -1, +3, +6, +8, +9, +10, +13, +16, +17, +18, +19

Oi = 9, 7,5, 3 , 1, 2, 5, 6, 7,5, 10, 11, 12, 13, 14

W= "Oi = 9+7,5+3+1 = 20,5

(20,5 + 0,5) - (14)(15)/4 21 - 52,5

Z = ---------------------------------- = --------------- = -1,98

"(14)(15)(28 + 1)/24 15,93

4.- Puesto que = 0,05:

W14,0,05 = 26 > 20,5, por lo que rechazamos H0.

Z0.05 = -1,64 > -1,98, por lo que se rechaza H0.

Hay evidencia suficiente para concluir que tras el retiro, aumenta el nivel de desajuste, medido por X.